前回は2D のTransformation Matixについて話しますが、次は3D Object Transformation Matrixですね。難しいそうですけど、できるだけ簡単でメモしようと思います。

3D空間でObjectを定義するにはいくつの変数が必要になるでしょうか。

正解は6つです。

[x,y,z]はObjectのPositionです。

[α,β,૪]はObjectのOrientation(向き)です。

ここにはx,y,zがあります。3D Objectではそのモデルで表現されます。

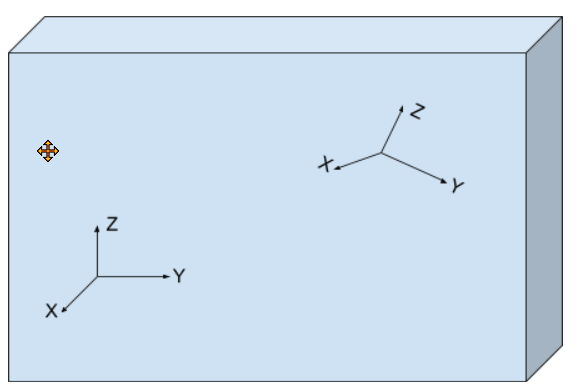
Right-Hand-Rules

次はそのルールについて話しいます。

https://www.pasco.com/products/guides/right-hand-rule

三本の指で3つのAxisが表現されています。

そしてRx(Φ),Ry(θ),Rz(ψ)と3つの数値で回すの角度を示しています。

Rx(Φ)はRollです。

Ry(θ)はPitchです。

Rz(ψ)はYawです。

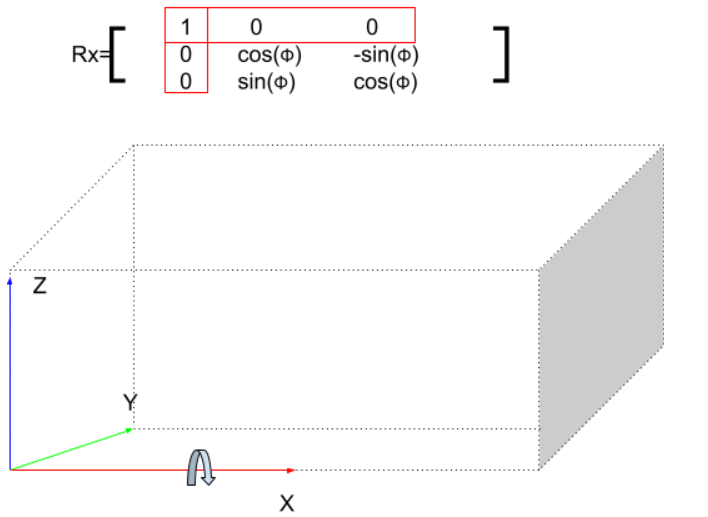
X Axis(Roll)

では、x軸が回転すると想像しましょう。

Xが回転してるってことはXが不変でYとZが変わってしまうのです。

その変わってしまうの計算は2D Object Transformation Matrixですね。

なので、3×3のMatrixはこうになります：

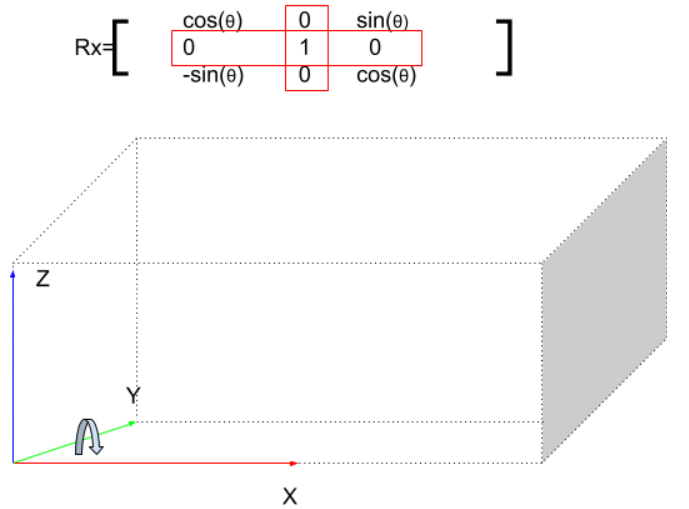
Y Axis(Pitch)

次はY軸です。X軸の回転と同じ不変になったのはYだけですね。

なので、3×3のMatrixはこうになります：

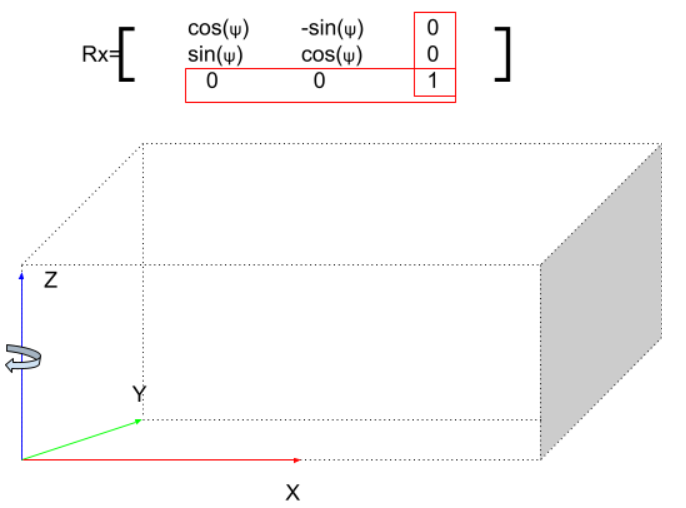
Z Axis(Yaw)

最後はZ Axisですね。

Rotationの表現

1つのRotationは最大3つのPatternがあります。

R(Φ,θ,ψ)

これらのRotationはどんな順番でもOKですが、一回目と二回目は同じ軸回転はNGです。

なぜかというと、R(Φ)R(Φ)=R(2Φ)です。

Total Pattern:3x2x2=12です。

xyz yxz zxy

xzy yzx zyx

xyx yxy zxz

xzx yzy zyz

ですね。

Euler Angles

すこく簡単にいいますと、最初と最後を回転したのは同じの軸のことです。

なので、

xyz yxz zxy

xzy yzx zyx

xyx yxy zxz

xzx yzy zyz

3x2x1=6組になります。

Cardan Angels

こっちらは回転する軸全部違うのことです。

xyz yxz zxy

xzy yzx zyx

xyx yxy zxz

xzx yzy zyz

計算

最後に、R(AB)=Rx(Φ)Ry(θ)Rz(ψ)だとします。

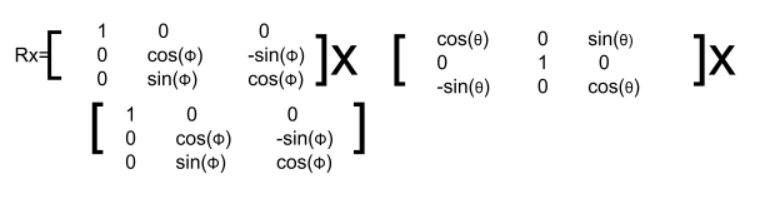
すべての式の結果はWikiに乗っています。

https://en.wikipedia.org/wiki/Euler_angles

では、T(source-Target)=(x,y,z,α,β,૪)となっており、式はこうになります。

はーい、お疲れ様です。

Reference

https://www.mathsisfun.com/algebra/matrix-inverse.html

https://www.rosroboticslearning.com/rigid-body-transformations

https://math.stackexchange.com/questions/1090451/why-is-ab-1-a-1b-1